Линейные уравнения с параметром, содержащие квадратные корни

Обратим внимание, что во всех решенных примерах областью допустимых значений как для переменной, так и для параметра являлось все множество действительных чисел. Разумеется, следует познакомиться с задачами иного рода.

Пример 1. Решить уравнение .

Решение. легко увидеть, что x=a – единственный корень данного уравнения. Однако, этот результат – еще не ответ. специфика уравнений с параметрами предполагает даже в таком тривиальном уравнении, как x-a=0, отмечать, что x=a – корень при любом a.

Ответ. Если a≥0, то x=a, если a<0, то нет решений.

Пример 2. Решить уравнение .

Решение. .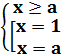

Отсюда x=a – корень исходного уравнения при любом a, а x=1 – корень лишь при a≤1.

Ответ. Если a<1, то x=0 илиx=1, если a=1, то x=1, если a>1, то x=a.

Пример 3. Выясните, при каких значениях параметра a данные уравнения имеют ровно один корень:

а) ;

б) .

а) .

Решение.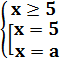

Отсюда x=5 – корень исходного уравнения при любом a≠5.

Ответ. x=5 при a≠5 – единственный корень.

б) .

Решение.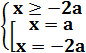

Отсюда , если a>0. И x=-2a, если a<0. Уравнение имеет единственный корень лишь при а<0.

Ответ. При а<0 x=-2a – единственный корень.

Пример 4. При каких а уравнение имеет единственное решение?

Решение. При любом а x=1 – корень данного уравнения, и требование единственности решения сводит задачу к поиску условий, при которых уравнению «запрещено» иметь корни, отличные от единицы. В то же время множитель x-a как бы предлагает еще один корень, и, на первый взгляд, значение a=1 представляется достаточным для ответа. Но более внимательный анализ позволяет «отмести» x=a за счет области определения уравнения: при a<0 x=a не является корнем.

Ответ. a=1 или a<0.

Пример 5. Решить уравнение .

Решение.

Если a=1, то корней нет.

Ответ. Если a≠1, то x=a, если a=1, то корней нет.

Пример 6. Решить уравнение .

Решение. x=0 или x-a=0. Откуда x=a. Причем, x-a≥0. Следовательно, x≥a.

Ответ. Если a<x, то x=0, если a=x, то xєR, если a>x, то решений нет.

Пример 7. Решить уравнение .

Решение. .

Ответ. Если

Пример 8. Решить уравнение .

Решение. Сумма двух корней может оказаться равной нулю лишь в том случае, если оба слагаемых равны нулю.

.

Ответ. Если a=0, то x=0, если a≠0, то решений нет.

Пример 9. Решить уравнение .

Решение. . Следовательно, .

.

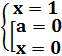Ответ. Если a=0, то x=1, если a≠0, то решений нет.

III.2 Классификация задач на решение квадратных уравнений с параметром

Выделим класс задач, где за счет параметра на переменную накладываются какие- либо искусственные ограничения. Для таких задач характерны следующие формулировки: при каком значении параметра уравнение имеет одно решение, два, бесконечно много, ни одного; решением уравнения является какое-то подмножество множества действительных чисел и другие.

Прежде всего сюда относятся уравнения второй степени. Поэтому, прежде всего, обратим внимание на распространенную ошибку: считать такое уравнение квадратным. На самом деле это уравнение степени не выше второй. Пользуясь этим соображением, естественно начать решение, рассмотрев случай, когда коэффициент перед x2 равен нулю. Итак, если параметр равен нулю, то, очевидно, данное уравнение имеет единственное решение. если же a≠0, то имеем дело с квадратным уравнением.